Heb ik nog genoeg stookolie ?
Print0Koud als het is peilde ik daarnet of we nog wel genoeg stookolie hebben om ons de volgende weken te kunnen verwarmen. Maar wacht, ik meet een hoogte in een cilindrische tank ! Ik weet wel dat het een tank is van drieduizend liter. En dat hij 120cm diameter heeft. Maar hoeveel stookolie zit er nu in als ik 25cm peil ? Vind het hier uit !
Geen wiskunde alstublieft !
Die wiskunde interesseert je geen knijt, maar je zou het ook wel willen weten voor je cilindrische tank ? Vul dan onderstaande gegevens in en ik bereken het wel even voor je.
Geef me toch maar de wiskunde !
De berekening hiervan is niet zo moeilijk en kan met wiskunde uit het middelbaar onderwijs. Uiteraard zijn er wel een aantal vereenvoudigingen. Ik ga er van uit dat de tank een perfecte cilinder is, die ook perfect horizontaal ligt. In werkelijkheid zijn er doorgaans welvingen op de koppen, maar die introduceren geen al te grote fout.
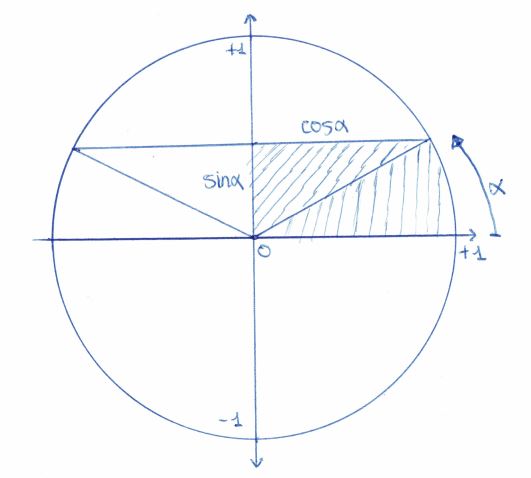De uitleg is aan de hand van deze tekening. De verhoudingen zijn gereduceerd tot een cirkel met straal 1.
Veronderstel dat het peil boven de helft staat zodat een hoek `alpha` wordt gevormd tussen de horizontale middellijn
en de stand van de stookolie. `alpha` drukken we uit in radialen ( `2*pi` radialen in een cirkel ). Rechts boven is dan een oppervlakte die bestaat uit het cirkelsegment en een rechthoekige driehoek.
De rechthoekige driehoek heeft als zijden `sin(alpha)` en `cos(alpha)`. Zijn oppervlakte is dus `1/2*sin(alpha)*cos(alpha)`.
Het cirkelsegment heeft als oppervlakte `pi/2*alpha`. Rechtsboven staat dus een gearceerde oppervlakte van :
Links boven is de oppervlakte wegens symmetrie dezelfde. Er staat dus een oppervlakte `sin(alpha)*cos(alpha)+alpha` boven de helft. Onder de helft uiteraard `pi/2`.
De oppervlakte gevuld door de stookolie ( na de verhoudingen tot een cirkel met straal 1 te hebben gereduceerd) is dus : `pi/2+alpha+sin(alpha)*cos(alpha)`. Met `I` de totale inhoud van de tank is de resterende inhoud dus :
Als de stookolie onder de helft gaat wordt `alpha` negatief en ook `sin(alpha)*cos(alpha)`, m.a.w. de formule blijft opgaan onder de helft. Blijft de vraag hoe aan `alpha` te komen. We zien dat `sin(alpha)` de peilhoogte is, waarbij -1 leeg is, 0 halfweg en +1 vol. Daaruit volgt dat, met `R` de straal van de tank en `P` de peilhoogte :
Geen reacties op “Heb ik nog genoeg stookolie ?”